Mathematical Physics

 Lesson No 02. Mathematical Physics

🕮 Introduction

In previous lesson we have studied about various physical quantities which can be measured.But all these quantities cannot be fully described by measurements and units only.There is a need to do perform mathematical operation to obtain a desired resultsThis physical quantities are described fully using magnitude,direction or both.In order to describe Physical Quantity , it has been categorized into two types:

a) Scalar Quantity

b) Vector Quantity

    🕮 Scalar Quantity

Scalar Quantity: Any physical quantity that depend only on magnitude and not on direction is called as Scalar Quantity . Eg: Mass , Work, etc

Let us consider an example , A person carrying 5kg sugar wants to go to a particular distance B. He can reach that point by going from any direction . After reaching point B the mass 5 kg remains unchanged ,thus it does not depend on direction ,hence mass is a scalar quantity.

Scalar quantity can be added, subtracted,multiplied,divided  by simple mathematical operations we use in our day to day life.

🕮 Vector Quantity

Vector quantity : Any physical quantity that depend  on magnitude as well as direction is called  as Vector Quantity. Eg : Force, Torque, Velocity, etc

Let us consider an example , for opening a particular door, minimum 5N force is required and it should be pulled but if a person is applying 5N force and he is pushing it instead of pulling ,then door will not be opened .On the other hand , if im pulling it a person is pulling it but applying force less then 5N ,again door will not be opened. So we can conclude that if we do not take magnitude as well as direction into consideration, we do not obtain the output  ,thus  force depends on magnitude as well as direction ,hence Force is a vector quantity.

🕮 Representation of a Vector

A vector quantity is represented by a directed line segment or we cam say ‘arrow’ .Let a person moves from point A to B, then it can be represented as,

                               AB

where A is starting point of the person called as tail of the vector and B is end point         called as head of the vector. It can be written as

🕮 Types of Vector

Zero Vector (Null vector) : A vector with zero magnitude with a particular direction is called as Zero Vector.

Symbol for Zero vector : 0

Examples for zero vector:

1.Velocity vector of a particle which is at rest is a zero vector

2.The acceleration vector of particle in motion with uniform velocity is zero vector

Resultant vector : The resultant of two or more vectors is that single vector, which produces the same effect, as produced by all the vectors together.

                                              

                              a + b is a resultant vector produced by Vector a and vector b

Negative Vector :A negative vector of a given vector is a vector of the same magnitude but directed opposite to that of the given vector.

                              

Vector CD is negative vector of AB

Equal Vector: Two vectors A and B representing same physical quantity are said to be equal if and only if they have the same magnitude and direction.

Position Vector : : A vector which gives the position of a particle at a point with respect to the origin of a chosen coordinate system is called the position vector of the particle. 

Vector OA And OB are position vectors

🕮 Unit Vector

Unit Vector : A vector having unit magnitude in a given direction is called as unit vector

Vector Operations

Addition or subtraction of two or more vectors of same type ,yield a single vector whose effect is same as net effect by the vectors which were added or subtracted.

🕮 Addition of a Vector

If individual vectors are parallel with same direction ,the resultant is obtained by adding the individual vectors

                    

🕮 Subtraction of a Vector

If individual vectors are parallel with opposite direction the resultant is obtained by adding the individual vectors.

🕮 Triangle Law for Vector Addition: 

If two vectors describing the same physical quantity are represented in magnitude and direction by the two sides of a triangle taken in order, then their resultant is represented in magnitude and direction by the third side of the triangle drawn in the opposite sense (from the starting point of first vector to the end point of the second vector).

🕮 Laws of  Vector Addition

 * Commutative Law : Vector Addition Obeys Commutative law

  a + b = b + a

* Associative Law : Vector addition obeys associative Law

🕮 Parallelogram Law of  Vector Addition

If two  vectors of the same type starting from the same point, are represented in magnitude and direction by two adjacent side of a parallelogram , then their resultant is represented in magnitude and direction by the diagonal of the parallelogram starting from the same point.

Mathematical Approach for Resultant of a vector starting from same point: 

Consider  two vector P and Q of same type starting from point O making an angle ɵ with each other.

Let us construct a seg BC and AC to complete a parallelogram OACB. As OA ll BC and OB ll AC ,

OB = AC = Q and OA = BC = P. We need to proof OC is a resultant .

---

Resolution of vector

The process of finding component of a vector is called as resolution of a vector. 

for eg:   A stone is thrown in direction other than vertical, the motion of the stone is defined by Resultant vector which is made up of two components.

This component can be found at any angle, but if the components are at right angle to each other it is called as Rectangular components.

Let see how to rectangular components are obtained,

From the figure above,

It is clear that OT is a resultant vector

Two perpendicular is drawn from T to meet N at Y-axis and M at X-axis.

R_x = OM 

and

R_y = ON

are the rectangular component of Resultant R along  the X-axis and Y-axis respectively.

By parallelogram law of vector addition,

R= R_x +  R_y

  R= R_x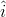  +  R_y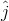

where 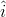   and 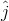  are unit vectors in x and y axis respectively.

If θ is the angle between Resultant and X-axis 

then

cosθ = OM / OT 

cosθ = R_x / R

Rcosθ =  R_x --------(1)

sinθ = MT / OT 

sinθ = R_y / R

Rsinθ =  R_y --------(2)

Squaring and adding equation (1) and (2)

R²sin²θ+R²cos²θ= R_x² + R_y²

R²(sin²θ+cos²θ) = R_x² + R_y²

R² = R_x² + R_y²

R= √ (R_x² + R_y²) ------A

Expression A gives magnitude of a resultant vector.

If there are three components  R_x^{2 ,}  R_y² , R_y²

then Equation changes to 

R= √ (R_x² + R_y² + R_z² ) 

Next: Scalar Product

---

Be  a winner : Every individual is a precious gift by god. Every individual is bestowed with infinite talent within him/her by nature. The human brain is a storehouse of  precious collections and this collections is the source to be a winner. Every individual when born start learning new thing, apply it and try to be a best version of himself/herself.Read More

Change Your life: Every people in this world want to be successful. Each individual is abided by the law of nature. The success of each individual is measured in terms of hard work and consistency. The higher the hard work and consistency , the higher is the rate of success. For being a successful person you(each individual)should constantly work on being a unique you(i.e Being different from others). Read More

The 80/20 principle : In our competitive world, each individual have a choice to live a better life, to have more than other. In order to make up with this demand they work harder and harder. But this technique do not yield the expected results, A student learning for 8 hours may  not obtain good grades in exam.Read More

Learn Game Development :  Computer as well as mobile Game had been on high demand nowadays and many gaming industries around the world face shortage of developers. Since many years Gaming industries have been taking over the market by proving game for android as well as windows phone. It has been a good source of earning as well as learning the behaviour .Read More

    

---