Uniform Circular motion

Uniform Circular motion

Introduction: Motion of a particle along the circumference of a circle with constant speed is called as uniform Circular Motion. For performing uniform circular motion, the velocity should have different direction. If acceleration is in line with velocity ,then the magnitude will change and the motion will no loner be a uniform circular motion. For changing direction of velocity there should be an acceleration which should be acting perpendicularly to tangential velocity. As this acceleration is acting towards center, it is called as centripetal acceleration. We will learn more about it in this section.

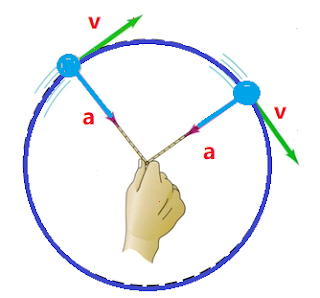Uniform Circular Motion

Expression for Centripetal Acceleration : From the diagram shown below

Centripetal acceleration

Consider a circular path with position vector r = OB. The position vector ωt can be resolved into two component, viz 

rcosθ (Horizontal component) and rsinθ (Vertical Component)

r = rcosθ + rsinθ

_{│<<<Projectile Motion│   │Conical Pendulum>>>│} 

---