Internal Energy

Internal Energy

Introduction : The total energy of the system is given by sum of its kinetic and potential energy, which exist due to motion and shape of the body. There exist an energy which is due to random motion of atoms and molecules of the system called as internal energy of the system. We are going to discuss this internal energy in details.

Internal energy of a system is defined as energy due to random and disordered motion of the molecules.

Internal energy of the system can be considered as the sum of kinetic energy, potential energy and vibrational energy of the molecules or atoms.

For eg: Let us consider a cup of tea which is placed on the table. Here you can see that cup is stationary which tells that kinetic energy of the body is zero, and as it is not displaced potential energy can be considered zero. On the other hand the molecule of the tea is in random motion due to some energy, this energy is called as internal energy of the body.

Internal energy of the body is mathematically calculated based on degree of freedom of the atom/ molecule. Let us understand degree of freedom., i

Mathematically , internal energy is expresses by 'U'.

---

Degree of Freedom : It is defined as total numbers of coordinates  or independent quantities required to describe the position and configuration of a system completely.

For monoatomic gases,

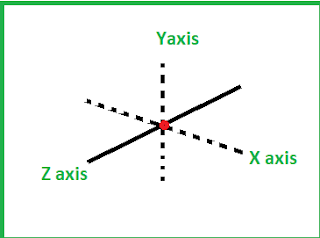
Let us consider Helium (He).It can move in three direction in a space i.e  in x , y, z direction. 

Thus it has only 3 degree of freedom.

Energy associated with each degree of freedom is 1/2KT

Total energy for monoatomic molecule will be 3/2KT

For diatomic gases,

Let us consider a diatomic molecule like Oxygen O₂  or Nitrogen N₂ ,

It is free to move in 3 translation direction i.e in x , y, z direction. In additional it is free to perform rotational motion around Y and Z direction, if molecule is situated on X axis. As it is situated on X axis it cannot rotate around X axis in the sense there will be no change in position of molecule while rotating on X axis.

Translation degree of freedom: 3

Rotational degree of freedom :2

Degree of freedom : 5

Energy associated with each degree of freedom is 1/2KT

Total energy for diatomic molecule will be 5/2KT

---

_{│<<<Thermal Equilibrium}││ _Heat>>>│ 

---