Specific Heat Capacity
 |
| Photo by Quino Al on Unsplash |
Introduction : We come across many phenomenon of heat in our day to day life.I t is our day to day observation that when we keep two different vessel, let say A and B of copper and aluminium of same mass respectively in heat for same amount of time having initial temperature same absorbs different amount of heat. we conclude that different material require different heat to make same change in temperature. The secret behind this is studied based on the observation of specific heat capacity.
Specific heat capacity : The amount of heat required to raise the temperature of 1kg mass of system by1℃ rise in temperature is called as specific heat capacity
Mathematically,
s = ΔQ / m ΔT
where s = specific heat capacity
ΔQ = Amount of heat absorbed or given
m = mass of the body
ΔT = change in temperature
if m =1kg and ΔT=1℃ then s = ΔQ
Molar Specific heat capacity : The amount of heat required to raise the temperature of 1mole of system by1℃ rise in temperature is called as specific heat capacity
Mathematically,
c = ΔQ / μ ΔT
where c = molar specific heat capacity
ΔQ = Amount of heat absorbed or given
μ = 1 mole
ΔT = change in temperature
if μ =1mole and ΔT=1℃ then c = ΔQ
SI unit of specific heat capacity is J / mol ℃
cgs unit of specific heat capacity is erg /mol ℃
Molar specific heat capacities of gases: In case of a gas, (for 1 mole) slight change in
temperature is accompanied with considerable
changes in both, the volume and the pressure.
If gas is heated at constant pressure, volume
changes and therefore some work is done on
the surroundings during expansion requiring
additional heat. As a result, specific heat at
constant pressure (Cp
) is greater than specific
heat at constant volume (Cv
).
a) Molar specific heat capacity of a gas at
constant volume (Cv
) is defined as the
quantity of heat absorbed or released for
the rise or fall of temperature of one mole
of the gas through 1K (or 1°C), when its
volume is kept constant.
for 1 mole of gas at constant volume dQ = Cv dT
b) Molar specific heat capacity of a gas at
constant pressure (Cp
) is defined as the
quantity of heat absorbed or released for
the rise or fall of temperature of one mole
of the gas through 1K (or 1°C), when its
pressure is kept constant.
or 1 mole of gas at constant pressure dQ = Cp dT
Mayer's Relation
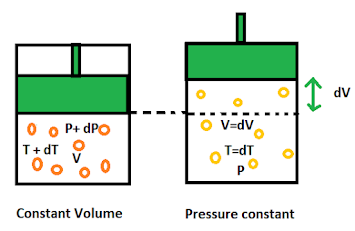
Consider 1 mole of gas enclosed in an container having frictionless piston in it. The gas is having pressure P ,volume V and temperature T.
Case I : The gas is heated to increase it's temperature from T to dT at constant volume. Due to rise in temperature the pressure increases and the internal energy of the system increases. The amount of heat supplied is used to increase the internal energy and no work is done in the system since, volume is constant.
dQ1 = dE = Cv dT ----------(1)
where Cv is the molar specific heat of the gas at constant volume.
Case II : The gas is heated to increase it's temperature from T to dT at constant pressure. Due to rise in temperature the volume increases and the internal energy of the system increases . The amount of heat supplied is used to increase the internal energy and work done to move the piston is.
dQ2 = dE + dW = Cp dT ----------(2)
where Cp is the molar specific heat of the gas at constant pressure.
from (1) and (2)
Cv dT + dW = Cp dT -----------( dE =Cv dT )
dW = (Cp - Cv) dT
P dV = (Cp - Cv) dT ---------( dW = P dV) -----(3)
now for 1 mole , ideal gas equation is
PV =RT------(4)
from (3) and (4)
R dT = (Cp - Cv) dT
R = ( Cp - Cv ) ------(5)
Equation (5) gives mayer's equation for 1 mole gas.







No comments:
Post a Comment