Expression for projectile Motion

 Expression for projectile Motion

Projectile Motion : An object thrown in the air with initial velocity in any direction, making some angle with the horizontal, moving freely under the action of gravity is called projectile.

Mathematically,

 

Consider displacement in horizontal direction,

Displacement = Velocity x time

X= ucosθ x t

t = X / ucosθ-----(1)

---

Time of Ascent (T_A): The time taken by a particle to reach maximum height is called as Time of Ascent.

---

Total time of projectile (T): The time taken by a projectile to complete one flight is called as time of projectile.

_{│<<<Projectile Motion│   │Uniform Circular Motion>>>│} 

---

Read More

Projectile motion

Projectile motion 

Introduction :  previous topic we have studied average and instantaneous velocity and acceleration. In our daily life we come across various motion like throwing a ball, footballer kicking a ball, motion of a giant wheel, etc. This type of motion is a motion in which system perform motion in two direction simultaneously. We are going to study how such type of motion happens in our nature.

Perform this interesting experiment by your own

Please wait loading!!

Credit : Phet University of colorado Boulder

Projectile Motion

Projectile Motion: An object thrown in the air with initial velocity in any direction, making some angle with the horizontal, moving freely under the action of gravity is called projectile.

Point of projection: The point from which the body is projected  in air is called as point of projection.

Velocity of projection: The velocity with which a body is projected is called as point of projection.

Angle of projection: The angle made by the velocity of projection with the horizontal is called as point of projection.

Trajectory: The path followed by the projectile in space is called as its trajectory.

Explanation: When projectile motion is formed , the initial velocity (u) is resolved into two components i.e horizontal component (ucosθ) and vertical component (usinθ). The acceleration due to gravity has no acceleration in horizontal direction thus there is no change in horizontal velocity. Thus projectile motion is a combination of two component of a motion  occuring simultaneously. viz: i) a vertical motion with constant acceleration and ii) horizontal motion with constant velocity.

_{│<<<Average velocity and Accelderation│   │Expression for Projectile Motion>>>│} 

---

Read More

Average Velocity and instantaneous velocity

Average Velocity and instantaneous velocity

Credit: Vasck.cz(Motion)

Introduction : We have studied about Motion in One dimension .i.e motion in a straight line (Rectilinear motion). Motion of a particle in straight line is governed by three kinematical equation (v = u + at) , v² = u² + 2as), (s = ut + 1/2 at²) which gives the relation between position, displacement, velocity and acceleration. Now in this topic we are going to learn in detail about position vector, displacement, velocity and acceleration in 2 dimension.

Position vector : Let us understand the position vector in 2 dimension. From the fig below, the position vector at time t₁ is OP = r and position vector at time t2 is OQ = r'. The change in positionn vector i.e , PQ is ∆r = r' - r . 

Thus mathematically, 

r = x î + y ĵ

r' = x' î + y' ĵ    

From Triangle law of vector addition,

OP + PQ = OR

r + ∆r = r'

∆r = r' - r

∆r = (x' î + y' ĵ ) - (  x î + y ĵ  )

∆r = ( x'  - x )  î + ( y' - y ) ĵ -----(A)

Equation (A) gives change in position vector  in 2 dimension.

---

Average velocity

The average velocity of  a particle performing motion in a plane is given by,

The instantaneous velocity of  a particle performing motion in a plane is given by,

---

_{Average acceleration}

_{From above diagram and expression}

_{Mathematically, average acceleration is given by,}

_{Mathematically, instantaneous acceleration is given by,}

_{│<<<Motion in a plane│   │Projectile Motion>>>│} 

---

Read More

Doppler Effect

Doppler Effect

Introduction : In our day to day life we come across lots of phenomenon like a train approaching toward us or moving away from us. We have noticed that as the train approach towards us we are able to hear the sound of high pitch and as the train moves away we are able to notice that the pitch of sound goes on decreasing. This change in the pitch was first studied by Christian Doppler and this phenomenon is called as Doppler Effect. We are going to understand this topic in detail.

Listener as well as Source is stationary

Listener is stationary and Source is approaching toward listener

Doppler Effect can be studied in three different cases:

1) Source Moving and Listener Stationary

2) Source  Stationary and Listener Moving

3) Source Moving and Listener Moving

1) Source Moving and Listener Stationary :

a) Source is approaching towards listeners

Source is approaching towards Stationary listener

let us consider a source of sound moving towards an stationary listener with velocity V_s. The source is producing frequency of ղ and wavelength λ, the aparant frequency heard by listener is ղ_a as shown in fig 2. As the source moves towards listener the wavelength reduces and changes to λ1 and the velocity of sound is V.

Mathematically,

From Fig,

---

b)  Source is moving away from listener

Source is moving away from Stationary listener

let us consider a source of sound moving away from a stationary listener with velocity V_s. The source is producing frequency of ղ and wavelength λ, the aparant frequency heard by listener is ղ_a as shown in fig 2. As the source moves away from listener the wavelength increases and changes to λ1 and the velocity of sound is V.

Mathematically,

From Fig,

<<< Quality of Sound

---

Read More

Quality of a sound

Quality of  a sound

Photo by NII on Unsplash

Introduction : In previous topic we have discussed about the factors affecting the velocity of a sound. In this topic we are going to discuss which parameter helps in understanding the quality of sound. We are going to discuss more about quality of sound in this topic.

Quality of the sound depends upon major three factors.

a) Pitch :  Pitch relates to the sharpness or shrillness of a sound . If the sharpness of the sound is more then sound is said to be highly pitched. The more the frequency ,more is the pitch. For eg. The difference heard in the voice of a women and men is due to difference in pitch. Voice of female is very sharp i,e they have high pitch whereas the voice of men is having low pitch i.e low frequency.

b) Timber : Timber refers to quality of a sound heard by a listener .We are able to guess the difference between the voice when the person is suffering from cold or cough. The quality of sound in a musical instruments are due to mixture of tones and overtones. The sound quality in this context mentioned  is called as Timbre.

c) Loudness : Loudness of any sound depends on the intensity of a sound. Intensity  of a sound is defined as Sound energy passing through a given a area per unit time.

I = E / At

I = P/A

Where 

I = Intensity

P = Power

A = Area

SI unit of Intensity is Watt / m²

The maximum intensity that any human ear can hear  is I_max = 10¹ Watt / m²

The minimum intensity that any human ear can hear  is I₀ = 10^-12 Watt / m²

Mathematical expression for Loudness of a sound

According to weber fechner,

The loudness (L) of a sound is directly proportional to  ( log₁₀ I )

For maximum Loudness,

L_max ∝  log₁₀ (I_max)  -----(1)

For maximum Loudness,

L₀ ∝  log₁₀ (I₀) -----(2)

From (1) and (2) subtracting

L_max - L₀   ∝  log₁₀ (I_max)  -  log₁₀ (I₀) 

L_max - L₀   = K  log₁₀ (I_max)  -  log₁₀ (I₀) 

---

_{│<<<Echo│   │Dopplers effect>>>│} 

Read More

Nodes and Antinodes

Nodes and Antinodes

Introduction : In previous topic we have seen about mathematical expression in case of stationary wave. The stationary wave is a resultant of  two opposite wave having same amplitude. In a stationary wave there exist a alternate point of minimum and maximum displacement. This point is called as node and antinode respectively. We are going to see this in details.

Nodes and Antinode

Node : The point of minimum displacement is called as node.

Condition for Nodes : At the point of node the displacement is zero i.e A=0

From the equation of stationary wave we have Amplitude as 

---

Node : The point of maximum displacement is called as Antinode.

Condition for Antinodes : At the point of Antinode the displacement is 2a i.e 

A=(+- 2a)

From the equation of stationary wave we have Amplitude as 

As the distance between alternate  Node and Antinode is λ/2

therefore, distance between Antinode and Node is λ/4

_{│<<<Stationary wave│   │Harmonics and Overtone>>>│} 

---

Read More

Stationary Wave

 Stationary Wave

Stationary Wave

Introduction :In previous topic we have seen that when two or more wave meet at the same point, superposition of waves take place and this superposition leads to formation of  a standing wave or beats under certain conditions. We are going to study standing wave in details in this topic.

Stationary Wave: When two identical progressive waves both travelling along the same path in opposite directions, interefere with each other, by superposition of waves resultant waves obtained in the form of loops ,is called a stationary waves.

Formation of stationary wave (Graphical Method)

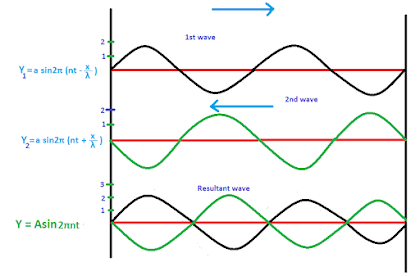Superposition of wave(stationary wave)

.Formation of stationary wave (Analytical Method)

From diagram above, consider two simple harmonic progressive wave with same amplitude and same frequency .

Y₁ = A₁ sin 2π (nt - x/λ)

Y₂ = A₂ sin 2π (nt + x/λ)

 The resultant displacement due to this two waves is given by,

Y = Y₁ + Y₂ 

_{│<<<Superposition of a wave│   │Nodes and Antinodes>>>│} 

Read More

Echo

Echo

Introduction : The sound wave travelling in the form of wave has the similar property of reflecting from a surface from where it is incident. The sound after reflection travels back towards the source and if it reflect again , the process goes on until the energy of the wave becomes zero. The reflection of the sound after reflection from rigid surface is called as Echo.

Condition for echo :  To hear a distinct echo , the  reflecting surface should be at a minimum distance of 17m (approx) from the source. the human brain have the tendency to retian any sound for about 0.1 second. If another sound reaches the human ear before 0.1 seconds , the sound is heard for prolong time and this phenomenon is called as reverberation.

At 22⁰C , the velocity of sound in air is 340m/s. The sound retains in the brain for about 0.1 second. Thus the distance for echo will be as,

Distance = Speed x time

Distance = 340 x 0.1

Distance = 34.4 m.

Thus the distance between source and sound would be half  i.e 17.2 m. 

_{│<<<Factors affecting velocity│   │Quality of sound>>>│} 

Read More

Factor affecting the velocity of wave

Factor affecting the velocity of sound

Velocity of a wave

Introduction : We are now aware of velocity of a mechanical wave explained by newton's and laplace. When the wave travel from one medium to another, the velocity changes as well as wavelength changes but frequency remains same. Theoretically, the velocity of the wave is same in same medium but practically it changes with changes in some atmospheric factor. We  are going to discuss the factors in details.

Effect of pressure on velocity of a sound : When sound travels in an air medium, then the change in pressure at constant temperature of the medium has no effect on velocity of the sound. 

Let us understand it mathematically,

According to Laplace's 

According to boyle's law at constant temperature ,Pressure remains constant.

From equation (1) we can conclude that the change in pressure at constant temperature of the medium has no effect on velocity of the sound.

---

Effect of temperature on velocity of a sound : When sound travels in an air medium, then the change in temperature of the medium result in change in velocity of the sound. 

 mathematically,

Let V and V₀ be the velocity of sound at 0°C and t°C respectively.

From Laplace equation,

From equation (A) we can conclude that velocity of sound in air is directly proportional to square root of its absolute temperature.

---

Effect of humidity on velocity of a sound : When sound travels in an air medium, then the change in humidity of the medium result in change in velocity of the sound. 

mathematically,

Let V_m and V_d be the velocity of sound in moist and dry air

respectively. 0°C and t°C respectively.

From Laplace equation, ρ_m and  ρ_d be the densities of  moist and dry air

respectively. 

Equation (A) concludes that speed of sound in moist air is greater than speed of sound in dry air. Thus speed of sound increases with increase in moisture.

proportional to square root of its absolute temperature.

_{│<<<Velocity of  a wave│   │Echo>>>│} 

---

Read More

Velocity of a wave

Velocity of a wave

Introduction : The progressive wave such as mechanical and electromagnetic wave has the parameter such as wavelength ,frequency, amplitude, etc. In this topic we are going to learn about velocity of  mechanical wave. The velocity of the mechanical wave plays a vital role in understanding the nature and mathematical concept. the velocity of  a mechanical wave depends upon elastic property and density of the medium. Let us study this in details.

Velocity of a wave

Velocity of transverse wave (on string) : The velocity of a transverse wave depends on the elastic property that is the restoring force in the medium. It also depends upon the linear mass density of the medium. In case of a string , the restoring force is the tension in the string.

Velocity of a transverse wave in string is directly proportional to square root of tension.

V ∝ √T ----(1)

Velocity of a wave in string is inversely proportional to square root of linear mass density.

From (1) and (2)

---

Velocity of longitudinal wave : Velocity of a longitudinal wave depends on the nature of compression and rarefaction. The compression and rarefaction is due to elastic property of the medium. Thus at compression the density of the medium is greater and at rarefaction it is quite lower. The conclusion gives the result that velocity of a longitudinal wave depends on the elasticity and  linear mass density.

Mathematically, 

where E  the modulus of elasticity of medium and ρ is the density of medium.

The sound waves travel in the medium. Therefore, according to Newton the heat is  developed during compression and cools during rarefaction. Thus the process is isothermal. Hence, isothermal elasticity to be considered .If the volume or bulk elasticity of air is  determined under isothermal change then it is called isothermal bulk modulus which is equal to the atmospheric pressure P. hence the above equation changes to ,

---

Laplace's correction : According to laplace ,newton's equation was not sufficient to explain the concept of velocity of a longitudinal wave. He was of the saying that the formation of  compression and rarefaction is not a slow process but it is very fast process and heat dissipation is not done completely. Thus the formation of rarefaction and compression was a adiabatic process and hence adiabatic elasticity should be considered. 

Adiabatic modulus of elasticity is given by E = үP.

where,

P = pressure of the air medium

γ = ratio of specific heat of air at constant pressure (Cp) to specific heat of air at constant volume (Cv) 

γ  = Cp / Cv

Thus the newtons equation changes to,

_{│<<<Superposition of wave│   │Factors affecting velocity>>>│} 

---

Read More