Atomic Radius

 Atomic Radius

From Bohr's Postulate, a mathematical expression for the radius of Bohr's orbit can be obtained. The distance between the center of the nucleus and the outermost orbit is called an atomic radius.

From Bohr's first postulate

Bohr's Atomic radius

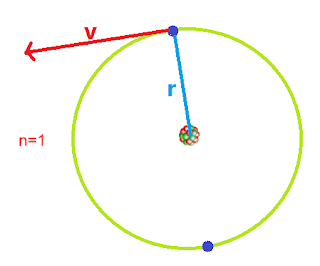
Consider an electron of mass m revolving around an atom of radius 'r' with velocity 'v'. Thus the centripetal force required for revolution is provided by the electrostatic force of attraction between the positive nucleus and negatively charged electron. Thus mathematically it can be written as

centripetal force = electrostatic force

From Bohr's second postulate:

Equation (C) gives an expression for atomic radius.

where,

h = planck' constant = 6.67 x 10^-34

𝛆₀ = 8.85x 10^-12

n= principal quantum number

m = mass of electron = 9.1 x 10^-31

e = elementary charge = 1.6 x 10^-19

for n= 1, i.e first orbit

Equ (E) gives the general equation for the radius of an orbit

 _{│<<< Bohr's Postulate││ Energy of an orbit>>>│}

---

Related Topics:  Atomic Structure      Geiger and Marsden Experiment     Atomic Spectra     Bohr's Postulate      Radius of an orbit      Velocity of an electron  Energy of an orbit      Limitation of Bohr's Model      De Broglie's explanation       Atomic Nucleus       Nuclear Binding energy        Radioactivity       Laws of radioactivity       Nuclear energy

---