Superposition of wave

Superposition of wave

Introduction : We are well aware of the parameter of a wave such as amplitude, frequency, wavelength, etc. Superposition of the wave is well understood by amplitude of a wave. Interesting phenomenon of superposition of a wave is due to two or more wave reaching simultaneously at a point. When sound wave travel from one medium to another their wave length as well as velocity changes, but frequency remains constant. 

Superposition of wave : when two or more waves, travelling through a medium, pass through a common point, independent of the presence of other wave. The resultant displacement at the point is equal to the vector sum of the displacements due to the individual wave at that point.

Superposition of wave

Analytical treatment of resultant of two wave.

From diagram above, consider two wave with different amplitude and same frequency  having phase difference of ф at x =0.

Y₁ = A₁ sinωt 

Y₂ = A₂ sin (ωt + ф)

 The resultant displacement due to this two waves is given by,

Y = Y₁ + Y₂ 

Y = A₁ sinωt + A₂ sin (ωt + ф)

Y = A₁ sinωt + A₂ sinωt cosф + A₂ sinф cosωt 

Y = (A₁ + A₂ cosф)sinωt  + A₂ sinф cosωt ----(1)

Let,

 (A₁ + A₂ cosф) = A cosθ ----(2)

and

A₂ sinф = Asinθ----(3)

from (1) , (2) , (3)

Y =  A cosθ sinωt  + Asinθ cosωt

Y =  Asin (ωt + θ)

Adding and squaring  (2) and (3)

A² cos²θ + A² sin²θ = (A₁ + A₂ cosф)² + (A₂² sin²ф )

A²  = A₁ ² + A₂²  cos² ф+ 2A₁ A₂+ A₂² sin²ф 

_{│<<<Expression of Progressive wave│   │velocity of  wave>>>│} 

---

Read More

Earth's Magnetism

Earth's Magnetism

Introduction : We are well aware of the magnetic field lines due to a magnet and the properties of magnetic field. Similarly earth behave like a huge magnet and show the properties similar to that of the bar magnet. In this topic we are going to discuss more about Earth's magnetism. When we hold a magnetic needle freely the needle comes to rest in geographical north and south direction, but if it was free to rotate in horizontal direction then ,it comes to rest making an angle with the horizontal. This indicate that there is an magnetic field on the earth.

Earth's Magnetism

A study of Earth's magnetic field is called as terrestrial magnetism. It is also called as Geomagnetism.

Parameter related to earth's magnetism:

Geographical Axis : A straight line passing through both the pole of the earth is called as Geographical axis.

Geographical meridian : At a give place it is vertical plane passing through the geographic north and south pole of the earth.

Geographic Equator : A plane perpendicular to the geographic axis is called as geographic equator.

Magnetic axis : A straight line passing through both the pole of the earth's magnet is called as Magnetic axis.

Magnetic Meridian :At a give place it is vertical plane passing through the magnetic north and south pole of the earth.

Magnetic Equator : A plane perpendicular to the magnetic axis is called as magnetic equator.

Note : The strength of the earth's magnetic field  on the surface of the earth is of the order of 10-4 tesla.

The direction of magnetic field at any location is specified by following

1) Magnetic Declination : The angle between magnetic meridian and geographic meridian at a place is known magnetic declination.

2) Angle of dip (ф) : The angle between earth's magnetic field at a place and the horizontal is known as the angle of dip at that place.

Magnetic Declination

---

IG : @physics_padhai

Read More

Magnetic field on equator

_{Magnetic field on equator}

Magnetic field on equator

Consider a bar magnet as given in  the figure above, having magnetic strength -m and +m seperated by a distance 2l. Let P be any point on the equator where magnetic induction is to be determined. Let the distance between Centre and point P is r. 

then from fig,

 l(OS) =  (ON) = l

NP²  = SP²  = r²+l²

^{Let Ø be the angle made by line NP and SP with axis of a dipole.}

^{The magnetic field at point P due to north pole is given by,}

^{The magnetic field at point P due to south pole is given by,}

The direction of B2 is along PS and represented by PT.

The component B1cosØ and B2cosØ are along diagonal PR and gets added .

thus resultant vector B is given by,

But from fig,

But for short dipole r>>>>l , higher power of l can be neglected

---

_{│<<<Magnetic field on Axis│   │Magnetic field at any arbitrary point>>>│}

---

Related Topics: Introduction   Magnetic Dipole Moment    Magnetic Field on-axis    magnetic field on equator    Magnetic field at any arbitrary point    Earth's Magnetism  

---

Read More

Expression of a progressive wave

Equation of a progressive wave

We are well aware of  a progressive wave, that a progressive wave continuously move in forward direction in a given medium without change in form. Since it is a progressive wave we need to understand this wave in form of time and displacement. As the progressive wave move in forward direction it is periodic in time as well as space hence it is a function of time and distance.

Progressive wave

In above figure the wave shown is transverse wave as it is periodic in space therefore position of the particle of the medium is described by fixes value of x. The displacement of a particle about its mean position is in Y direction. General equation of displacement of a particle from mean position is given by ,

Y = A sinθ

* For a progressive wave moving in right direction, the equation for sinusoidal wave is given by

Y(x,t) = A sin ( Kx -ωt+Φ)----(1)

As K = 2π/λ   and  ω =2π/T----(2)

from (1) and (2)

Y(x,t) = A sin [(2π/λ)x - (2π/T)t+Φ] 

At a particular instant say t = t₀ , 

 y (x, t₀ ) = a sin (kx - ωt₀  + φ) 

 y (x, t₀ ) = a sin (kx + constant ) 

 Thus the shape of the wave at t =t₀, as a function of x is a sine wave. 

Also, at a fixed location x = x₀  ,

 y (x₀ ,t) = a sin (kx₀  -ωt + φ) 

y (x₀ ,t) = a sin (constant - ωt) 

Hence the displacement y, at x = x₀  varies as a sine function. 

* For a progressive wave moving in left direction, the equation for sinusoidal wave is given by

Y(x,t) = A sin ( Kx + ωt+Φ)----(3)

As K = 2π/λ   and  ω =2π/T----(4)

from (3) and (4)

Y(x,t) = A sin [(2π/λ)x + (2π/T)t+Φ] 

Note : (kx - ωt + φ) is the argument of the sinusoidal wave and is the phase of the particle at x at time t.

_{│<<<Progressive wave│   │Superposition of wave>>>│}    

---

Read More

Magnetic Dipole Moment

Magnetic Dipole Moment

Bar Magnet

Consider a bar magnet as given in the figure above, having magnetic strength -m and +m separated by a distance of 2l. From the figure, we can define magnetic dipole moment as:

Magnetic Dipole Moment is defined as the product of its pole strength and its magnetic length.

Mathematically,

M = m . 2l

M = Magnetic dipole moment

m = pole strength

2l = distance between two poles

SI unit  is Am²

---

_{│<<<Magnetism│   │Magnetic field on axis>>>│}   

 

---

Related Topics: Introduction   Magnetic Dipole Moment    Magnetic Field on-axis    magnetic field on equator    Magnetic field at any arbitrary point    Earth's Magnetism  

---

Read More

Magnetism

Magnetism

Introduction : Concept of magnet was studied by many scientist like William Gilbert (1544- 1603), Danish physicist Hans Oersted (1777- 1851),  James Clerk Maxwell (1831-1879) . But the applications of magnet has been develop in late 19th century which had led the industrial revolution  a step ahead. In lower classes we have learned about magnet and general behaviour of a magnet i.e when same poles of a magnet are brought together they repel each other and when unlike poles are brought together they attract each other. Let us under the properties of magnet in detais in this topic.

Try this interesting experiment by your own

Loading please wait........

Credit:  weelookang@gmail.com;  Francisco Esquembre; Felix J. Garcia Clemente; Coco; Siti

Concept related to magnet

1) When a magnet is freely suspended using a string, it comes to rest in geographical north south direction.

2) Two poles of the magnet cannot be sepearted from each other.

3)The magnetic strength is always located at the pole.

4)Every magnet has a two poles i.e north and south pole.

---

Magnetic field lines :

Magnetic lines of force

PROPERTIES OF MAGNETIC FEILD LINES :

1) Magnetic field lines always originate from north pole and terminates at south poles. Inside a magnet the field lines is from south to north pole. It always form a closed loop.

2)The direction of the net magnetic field 'B' at a point is given by the tangent to the magnetic line of force at that point in the direction of line of force.

3) The number of magnetic field line per unit area gives the magnitude of magnetic field.

4)No magnetic field lines can intersect with each other.

Parameter related to magnetic field :

The strength of a magnetic field is expressed in terms of vector quantity called as magnetic induction (Magnetic field) B.

Magnetic field (B) at a given point is defined as magnetic flux per unit area.

Mathematically,

B = ф/ A

 SI unit is Tesla or weber/m²

Magnetic flux (ф) number of magnetic field lines passing normally through a given area.

Mathematically,

ф= B.A

 SI unit is Weber 

---

Concept of a bar magnet

Bar magnet

Axis : It is the line passing through both the poles of the magnet.

Equator : A line passing through centre of a magnet and perpendicular to the axis is called as equator.

Magnetic Length(2l) : The distance between two poles of the magnet is called as magnetic length.

---

 _{│Dipole Moment>>>│}    

---

Related Topics: Introduction   Magnetic Dipole Moment    Magnetic Field on-axis    magnetic field on equator    Magnetic field at any arbitrary point   Earth's Magnetism  

---

Read More

Progressive waves

Progressive waves(Mechanical)

Introduction : We are well aware of wave and types of wave i.e electromagnetic and mechanical wave. This mechanical wave are the wave which require material medium for it's propagation. In this topic we are going to see different types of progressive waves and their properties. 

Definition :Wave which travel continuously in a same direction in a given medium without change of form is called as progressive wave. There are two types of progressive  wave viz.

Perform this interesting experiment by your own

Please wait loading........

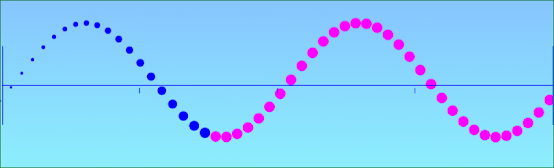
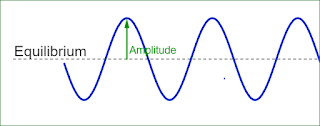
A) Transverse wave : wave in which the direction of vibration of particles of the medium is perpendicular to the direction of propagation of the wave is called as transverse wave. Eg: ripples on water surface.

Transverse wave

Properties of Transverse wave :

1) All particles of the medium  vibrate in a direction perpendicular to the direction of propagation of the wave with same period and amplitude.

 2) When transverse wave passes through a medium, the medium is divided into alternate crests and troughs . 

 3) Crests and troughs advance in the medium and are responsible for transfer of energy. 

4) Transverse waves can travel through solids and on surfaces of liquids only. They can not travel through liquids and gases.  

5) When transverse waves advance through a medium there is no change in the pressure and density at any point of medium, however shape changes periodically.

 6) If vibrations of all the particles along the path of a wave are constrained to be in a single plane, then the wave is called polarised wave. Transverse wave can be polarised. 

7) Medium conveying a transverse wave must possess elasticity of shape.

---

B) Longitudinal wave: wave in which the direction of vibration of particles of the medium is parallel to the direction of propagation of the wave is called as longitudinal wave.

Longitudinal wave

Properties of Longitudinal wave :

1) All the particles of medium  vibrate in a direction parallel to the direction of propagation of wave with same period and amplitude. 

2) When longitudinal wave passes through a medium, the medium is divided into regions of alternate compressions and rarefactions. 

 3) A compression and adjacent rarefaction form one cycle of longitudinal wave. The distance measured along the wave between any two consecutive points having the same phase is the wavelength of wave.

 4) For propagation of longitudinal waves, the medium should possess the property of elasticity of volume. Thus longitudinal waves can travel through solids. liquids and gases. Longitudinal wave can not travel through vacuum or free space. 

5) The compression and rarefaction advance in the medium and are responsible for transfer of energy. 

6) When longitudinal wave advances through a medium there are periodic variations in pressure and density along the path of wave and also with time. 

7) Longitudinal waves can not be polarised, as the direction of vibration of particles and direction of propagation of wave are same or parallel. 

_{│<<<Sound wave│   │Equation of  wave>>>│}    

---

Read More

Type of semiconductor

Type of semiconductor

From the previous topic we are well aware of  semiconductor, conductor and insulator and how they differ in terms of conductivity. In this topic we are going to see about semiconductor in details.

Semiconductors can be classified into two types viz. 

a) Intrinsic semiconductor :Extremely pure semiconductor are called as Intrinsic semiconductor. Eg: pure silicon, germanium. 

Let us understand Intrinsic semiconductor in details using diagram.

Intrinsic semiconductor at absolute zero temperature .Fig A

Silicon atom has 4 electron in its outermost orbit. As shown in the fig A each silicon atom share each electron with neighbouring silicon atom to complete their octet. Thus every silicon atom in a silicon lattice has a covalent bond between each other. At absolute zero temperature there is no free electron available for conduction and thus intrinsic semiconductor behaves as a insulator.

Intrinsic semiconductor at higher temperature. Fig B

As seen in fig B, as soon as the temperature is heated ,this covalent bond are broken and thus the valence electron becomes conduction electron. This removal of valence electron from orbit creates a vacancy in the band called as holes and it behaves as if it a positive charge.Thus every broken bond has equal number of free electrons and holes. n_e = n_h. As soon as potential difference is applied ,these electrons and holes contribute to electric current.

---

b) Extrinsic semiconductor : When intrinsic semiconductor is added with pentavalent or trivalent impurity we get extrinsic semiconductor. 

Extrinsic semiconductor (Lattice structure) 

Thus we can obtain extrinsic semiconductor by adding impurities to intrinsic semiconductors.

# The process of adding impurities to intrinsic semiconductor is called as doping.

# The impurities added are called as dopants.

Extrinsic semiconductor can be further classified into two types viz.

a) P type semiconductor : When Si or Ge crystal is doped with trivalent impurity such as indium(In), boron(B), aluminium(Al),we get P-type semiconductor.

p type semiconductor with indium as impurity

In above fig, we can see indium is added as a trivalent impurity. As indium has 3 electro in it's outermost orbit, 3 covalent bond are formed between indium and silicon atom. But the bond between indium and 4th neighbouring silicon atom has a vacancy which is called as hole. Thus this vacancy can accept one electron and called as acceptor impurity. At room temperature due to thermal energy this a electron can jump into holes thus leaving a hole at the place from where it jumps and contribute to current. Thus each hole is created for each impurity added. As p type semiconductor has large number of holes it is called as P type semiconductor(positive). Thus holes act as a majority charge carrier and electrons act as a negative charge carrier. Mathematically, n_e << n_h.

b) N type semiconductor :When Si or Ge crystal is doped with pentavalent impurity such as Arsenic(As), Antimony(Sb), Phosphorus(P),we get P-type semiconductor.

n type semiconductor with antimony as impurity

In above fig, we can see Antimony (Sb) is added as a pentavalent impurity. As antimony has 5 electro in it's outermost orbit, 4 covalent bond are formed between antimony and silicon atom. But the bond between 5th electron is with core which is broken at normal room temperature. Thus 1 electron each from antimony is available as free electron for conduction and thus it is called as donor impurity. Thus each free electron is created for each impurity added which contribute to electric current. As n type semiconductor has large number of electrons it is called as N type semiconductor(negative). Thus holes act as a minority charge carrier and electrons act as a majority charge carrier. Mathematically, n_e>> n_h.

_{│<<<Semiconductor│    │P-N Junction>>>│}

---

Read More

Sound

Sound

Photo by Brett Jordan on Unsplash

Introduction : We are well aware of  sound from our TV system, many audio system, This sound is a form of energy which travels in the form of wave. The wave is a system in which there is a transfer of energy and momentum without the transfer of particle. This wave is of different type depending upon dependence of propagation. Light is a type of wave, Sound is a type of wave. Before studying sound wave let us understand different type of wave.

Wave : Wave is described as a disturbance which involve transfer of energy without the transfer of matter.

Different types of waves: 

1) Mechanical wave : A wave that require a material medium for its propagation is called as mechanical wave. eg: sound wave, water wave, etc.

Mechanical wave

2) Electromagnetic wave : A wave that do not require material medium for it's propagation is called as electromagnetic wave. These waves are the result of vibration of electric and magnetic field. eg:  light, x-ray, etc.

Em wave

3) Matter wave : An object in motion is associated with an wave. Such wave is called as matter wave. This wave is related to quantum mechanics.

Progressive wave : Travelling or progressive waves are waves in which a disturbance created at one place travels to distant points and keeps travelling unless stopped by some external force.

---

_{Parameter of  a wave}

_{1) Amplitude (A): Maximum displacement of  a particle from its mean position is called as Amplitude.}

_{2) Frequency (}ղ) number of wave formed in one second is called as frequency . ղ= 1/T

_{3) Wavelength (λ) : The distance between two successive particles which are in same state of oscillation}

_{4) Time period (T) : The time taken by a particle to form one wave is called as time period. T = 1/}ղ

5) Velocity (v): Distance covered by a wave per unit time is called as velocity.

V = ղλ

                                          _{│<<<Types of mechanical wave│}

---

Read More